Heights and Distances

Heights and Distances Heights and Distances

Height and Distances

For knowing height and distance we must be well conversant with trigonometrical functions with measurement of angles. More specially if we can remember all formulas and measure of angles in tangent we must be able to solve all relating problems to height and distance.

Trigonometry is the study of relationships between the sides and angles of a triangle. We will study some ratios of the sides of a right triangle with respect to its acute angles, called trigonometric ratios of the angle. We will restrict our learning to acute angles only.

Trigonometric Ratios:

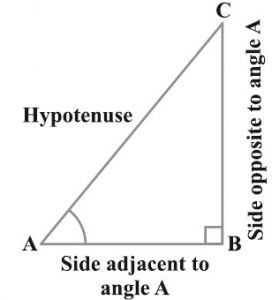
In above right angled triangle, angle A is acute, angle C is acute and angle B = 90 degree.

Side AC is the hypotenuse of the right angled triangle and the side AB is a part of angle A. We call it the side adjacent to angle A.

sin A = $\frac{side \opposite\ to\ angle\ A}{hypotenuse}$ = $\frac{BC}{AC}$

cos A = $\frac{side \adjacent\ to\ angle\ A}{hypotenuse}$ = $\frac{AB}{AC}$

tan A = $\frac{side\ opposite\ to\ angle\ A}{side\ adjacent\ to\ angle\ A}$ = $\frac{BC}{AB}$

cosec A = $\frac{1}{sin A}$ = $\frac{hypetnuse}{angle\ opposite\ to\ angle\ A}$ = $\frac{AC}{BC}$

sec A = $\frac{1}{cos A}$ = $\frac{hypetnuse}{side\ adjacent\ to \ angle\ A}$ = $\frac{AC}{BC}$

cot A = $\frac{1}{Tan A}$ = $\frac{cos A}{sin A}$ = $\frac{Side \adjacent\ to\ angle\ A}{side\ opposite\ to\ angle\ A}$ = $\frac{AB}{BC}$

Also tan A = $\frac{BC}{AB}$ = $\frac{sin A}{cos A}$

According to Pythagoras theorem in above right angled triangle ,

(AC)²= (AB)²+ (BC)²

Dividing by (AC)²in both sides, we get,

1 = sin²A + cos²A

Since sin A = $\frac{BC}{AC}$

and cos A = $\frac{AB}{AC}$

So sin²A = 1 – cos²A, and cos²A = 1 – sin²A

Similarly sec²A – tan²A = 1

So sec²A = 1 + tan²A and tan²A = sec²A – 1

Also cosec²A – cot²A = 1

So cosec²A = 1 + cot²A and cot²A = cosec²A – 1

tan(A+B) = $\frac{tanA + tanB}{1 - tanA . tanB}$

tan(A-B) = $\frac{tanA - tanB}{1 + tanA . tanB}$

cot(A+B) = $\frac{cotA cotB - 1}{cotA + cotB}$

cot(A-B) = $\frac{cotA cotB + 1}{cotB - cotA}$

sin2A = 2sinA. cosA = $\frac{2 tanA}{1 + tan^2 A}$

cos2A = cos²A – sin²A =2cos²A -1 = 1 – 2sin²A = $\frac{1 - tan^2 A}{1 + tan ^2 A}$

tan2A = $\frac{2tanA}{1 - tan^2 A}$

tan3A = $\frac{3tanA -tan^3 A}{1 - tan^2 A}$

A	0	30	45	60	90
Sin	0	1/2	1/$\sqrt{2}$	$\sqrt{3}$/2	1
Cos	1	$\sqrt{3}$/2	1/$\sqrt{2}$	1/2	0
Tan	0	1/$\sqrt{3}$	1	$\sqrt{3}$	Not defined
Cosec	Not defined	2	$\sqrt{2}$	2/$\sqrt{3}$	1
Sec	1	2/$\sqrt{3}$	$\sqrt{2}$	2	Not defined
Cot	Not defined	$\sqrt{3}$	1	1/$\sqrt{3}$	0

Angle of elevation

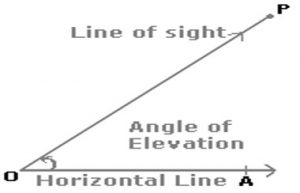
Suppose a man from a point ‘O’ looks up at an object ‘P’, placed Above the level of his eye. Then, the angle which the line of sight makes with the horizontal through ‘O’, is called the ’Angle of Elevation’ of ‘P’ as seen from ‘O’. Hence angle of elevation of ‘P’ from ‘O’ is <AOP.

Angle of Depression

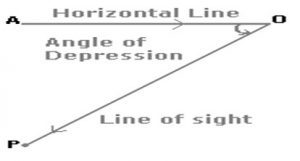
Suppose a man from ‘ O’ looks down at an object ‘P’, placed below the level of his eye. Then, the angle which the line of sight makes with the horizontal through ‘O’, is called the ’Angle of Depression’ of ‘P’ as seen from ‘O’.A

Hence angle of depression of ‘P’ from ‘o’ is <AOP.

Example-1

Two ships are sailing in the sea on the two sides of a light house. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the light house is 100 m high, the distance between the two ships is:

Ans- In side picture, let AB be the lighthouse and C and D be the positions of the ships.

Then AB = 100 m, <ACB = 30° and <ADB = 45°

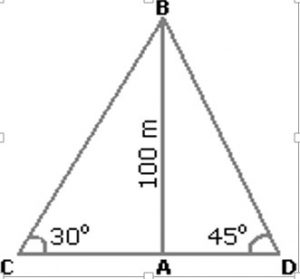
Hence AB/AC = tan 30° = 1/√3

Hence AC = AB √3 = 100√3 m.

Also AB/AC = Tan 45° =1 => AD = AB = 100 m

Now CD = CA + AD = 100√3 m. + 100 m = 100(√3 + 1)

=> 100 (2.732) = 273.2 say 273 m. (Ans)

Example-2

The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:

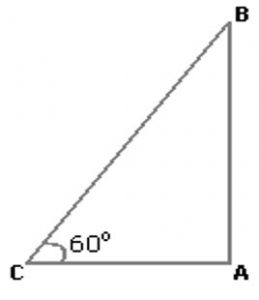
Let AB be the wall and BC be the ladder.

Then <ACB = 60° and AC = 4.6m

=>AC/BC = cos 60º = 1/2

=>BC = 2 AC = 2 × 4.6m

= 9.2m (Ans.)

Example 3: Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:

Solution:

Let AB be the lighthouse and C and D be the positions of the ships.

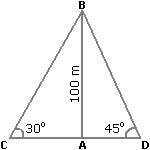
Then, AB = 100 m, ACB = 30° and ADB = 45°.

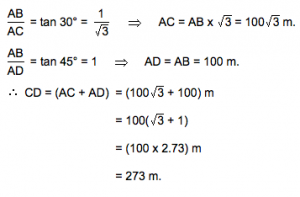
Example 4: A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30º with the man’s eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 60º. What is the distance between the base of the tower and the point P?

Solution:

One of AB, AD and CD must have given.

So, the data is inadequate.

Example 5: An observer 1.6 m tall is 203 away from a tower. The angle of elevation from his eye to the top of the tower is 30º. The heights of the tower is:

Let AB be the observer and CD be the tower.