Circle and Semicircle

Circle and Semicircle Circle and Semicircle

CIRCLE

A circle is the locus of all points equidistant from a central point called center.

Radius

The radius of the circle is a line segment from the center of the circle to a point on the circle.

radius

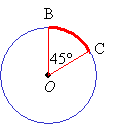
In the above diagram, O is the center of the circle and and are radii of the circle. The radii of a circle are all the same length. The radius is half the length of the diameter.

ARC

An arc is a part of a circle.

In the diagram above, the part of the circle from B to C forms an arc. It is called arc BC.

An arc can be measured in degrees. In the circle above, the measure of arc BC is equal to its central angle BOC, which is 45°.

Semicircle, Minor Arc and Major Arc

A semicircle is an arc that is half a circle. A minor arc is an arc that is smaller than a semicircle. A major arc is an arc that is larger than a semicircle.

Tangent

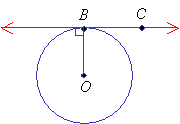
A tangent to a circle is a line that touches a circle at only one point. A tangent is perpendicular to the radius at the point of contact.

In the above diagram, the line containing the points B and C is a tangent to the circle.

It touches the circle at point B and is perpendicular to the radius

is perpendicular to i.e.

Secant

A secant is a straight line that cuts the circle at two points. A chord is the portion of a secant that lies in the circle.

Sector

A sector is like a “pizza slice” of the circle. It consists of a region bounded by two radii and an arc lying between the radii. The area of a sector is a fraction of the area of the circle

The formula to calculate the area of a sector is

The circumference of a circle

Perimeter of Circle

For any circle with a diameter, d, the circumference, C, is found by using the formula C = $\pi$ d

For any circle, the diameter is twice the radius, or d = 2 r.

The radius instead of the diameter we use the formula – C = 2 $\pi$ r

The area of a circle

For any circle with radius, r, the area, A, is found using the formula A = $\pi$ r²

SEMICIRCLE

Image result for semicircle

The perimeter of a semicircle

The perimeter is the distance round the outside. A semicircle has two edges. One is half of a circumference = $\frac{1}{2}$ $\pi$ d and the other is a diameter ‘d’.

= $\frac{1}{2}$ $\pi$ d + d or we say, πR + 2R where R is the radius.

The area of a semicircle

A semicircle is just half of a circle. To find the area of a semicircle we just take half of the area of a circle.

A = $\frac{1}{2}$ $\pi$ r²

Question – 1

Find the circumference of the circle with a diameter of 8 inches.

The circumference of the circle is 8π ≈ 25.163 inches.

Question2

Find the area of the semi-circle whose radius is 7 cm.

Solution:

Area of Semi-circle = (1/2) $\pi$ r²

Here r= 7 cm and $\pi$ = 22/7

= (1/2) × (22/7) × 7²

= (1/2) × (22/7) × 7 × 7

= 1 × 11 × 7

= 77 cm²

Question3

Find the circumference of the semi-circle whose diameter is 42 cm.

r = diameter/2

r = 42/2

r = 21

here r = 21 and $\pi$ = 22/7

= (22/7) × 21

= 22 × 3

= 66 cm

Question4

Find the area of the circle which is having the radius 21 cm.

Area of circle = $\pi$ r ²

= ( 22/7 ) × ( 21 )²

= (22/7) × 21 × 21

= 22 × 3 × 21

= 66 × 21

= 1386 cm²

Therefore the area of the given circle is 1386 cm²